
In this article, we will learn How to use the CONFIDENCE.NORM function in Excel.
What is confidence level and confidence interval?
In Statistics, when working with a normal distribution dataset. We find the sample mean of the sample dataset. For example finding the probability of winning the upcoming election by republicans or democrats. Or finding the amount of lead containing maggi packets is higher than the given limit. For these problems where the population dataset is infinite we calculate the values for the sample of data and predict the analysis for the population dataset. This interval around mean is also called the margin of error. Let's take an example where sample data (n) and calculate its mean (X) and standard deviation ( S ). Now to predict the estimation for the mean for the larger dataset, we use an interval called confidence interval around given confidence level. So the resulting confidence interval comes to be.
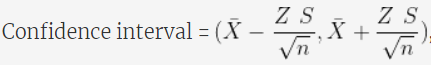
Here Z is a numerical value calculated based on the alpha (alpha = 1- confidence level). For 95% of confidence level, alpha comes out to be 0.05 and Z= 1.96. Mathematically we use the Z table to calculate the Z value. To calculate the confidence interval we need to calculate the margin of error and subtracting error value from mean value will give the lower limit of interval and adding the error value to mean value will give the upper limit of the interval. Let's calculate the margin of error in Excel using the CONFIDENCE.NORM function.
CONFIDENCE.NORM Function in Excel
CONFIDENCE.NORM takes the 3 numerical argument value of alpha, standard deviation and size of the sample dataset. The function returns the margin of error for the given alpha value. Let's understand these arguments stated below
CONFIDENCE.NORM Function syntax:
| =CONFIDENCE.NORM( alpha, standard_dev, size) |
alpha : value calculated using confidence level. 1 - confidence level
standard_dev : standard deviation for the given dataset.
size : sample size for the dataset.
Example :
All of these might be confusing to understand. Let's understand how to use the function using an example. Here we are given mean, standard deviation and size of the dataset.
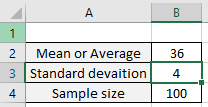
Now we calculator the margin of error for the confidence level 90%. Alpha would be calculated using the formula (1-confidence level). Use this alpha argument in the formula stated below
Use the formula for 90% confidence level:
| =CONFIDENCE.NORM ( E2, B3, B4) |

The function returns the value 0.6579 which will be the margin of error for the 90% confidence level. Now calculate the margin of error for the 95% & 99% confidence level.
Use the formula for 95% confidence level:
| =CONFIDENCE.NORM ( E3, B3, B4) |
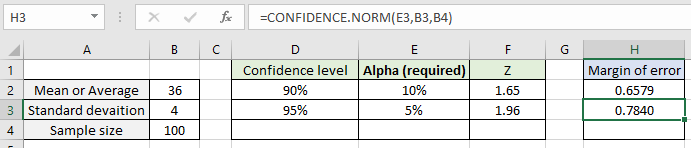
Similarly for the confidence level 99%. Use the alpha argument not the confidence level argument in the formula.
Use the formula for 99% confidence level:
| =CONFIDENCE.NORM ( E3, B3, B4) |

As you can see, increasing the confidence level, alpha decreases but the margin of error increases. Now calculate the confidence interval around the mean for the dataset.
Use the formula for lower limit of interval :
| = 36 - H2 |
Use the formula for upper limit of interval :
| = 36 + H2 |
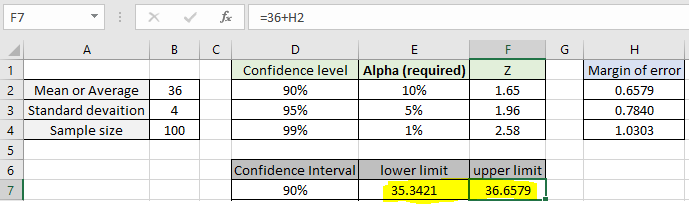
Confidence interval for the 90%confidence level comes out to be [35.3421, 36.6579]. This gives a good idea for the overall population dataset. Similarly find out the confidence interval for different confidence level stated.

As you can see all the intervals are around the sample mean.
Here are all the observational notes using the CONFIDENCE.NORM function in Excel
Notes :
Hope this article about How to use the CONFIDENCE.NORM function in Excel is explanatory. Find more articles on statistical formulas and related Excel functions here. If you liked our blogs, share it with your friends on Facebook. And also you can follow us on Twitter and Facebook. We would love to hear from you, do let us know how we can improve, complement or innovate our work and make it better for you. Write to us at info@exceltip.com.
Related Articles :
How To Use Excel T TEST Function in Excel : The T.TEST function is used to determine the confidence of an analysis in Excel. Mathematically, it is used to know if the mean of the two samples are equal or not. T.TEST is used to accept or reject the null hypothesis.
How to use Excel F.TEST Function in Excel : The F.TEST Function is used to calculate F statistic of two samples in excel internally and returns the two tailed probability of the F statistic under Null Hypothesis.
How to use the DEVSQ Function in Excel : DEVSQ function is a built-in statistical function to calculate the sum of squared deviations from the mean or average of the given distribution provided.
How to use Excel NORM.DIST Function : Calculate the Z score for the normal cumulative distribution for the pre specified values using the NORMDIST function in Excel.
How to use Excel NORM.INV Function : Calculate the inverse of Z score for the normal cumulative distribution for the pre-specified probability values using the NORM.INV function in Excel.
How to calculate Standard Deviation in Excel : To calculate the standard deviation we have different functions in Excel. The standard deviation is the square root of the variance value but It tells more about the dataset than variance.
How to use the VAR function in Excel : Calculate the variance for the sample dataset in excel using the VAR function in Excel.
Popular Articles :
How to use the IF Function in Excel : The IF statement in Excel checks the condition and returns a specific value if the condition is TRUE or returns another specific value if FALSE.
How to use the VLOOKUP Function in Excel : This is one of the most used and popular functions of excel that is used to lookup value from different ranges and sheets.
How to use the SUMIF Function in Excel : This is another dashboard essential function. This helps you sum up values on specific conditions.
How to use the COUNTIF Function in Excel : Count values with conditions using this amazing function. You don't need to filter your data to count specific values. Countif function is essential to prepare your dashboard.
The applications/code on this site are distributed as is and without warranties or liability. In no event shall the owner of the copyrights, or the authors of the applications/code be liable for any loss of profit, any problems or any damage resulting from the use or evaluation of the applications/code.